有临
2023.03.02
2421
在统计分析中我们常接触到线性回归模型和广义线性回归模型，但它们都要求因变量是连续的正态分布变量，自变量和因变量有线性关系。若因变量为分类型变量，而自变量与因变量却没有线性关系时，线性回归模型的假设条件不再适用。此时，Logistic回归模型是最好的选择，它对因变量的分布没有要求，从数学角度看，Logistic回归模型非常巧妙地避开了分类型变量的分布问题，补充完善了线性回归模型和广义线性回归模型的缺陷。从医学研究角度看，Logistic回归模型解决了一大批实际应用问题，对医学的发展起着举足轻重的作用。
Logistic回归模型
医学中常研究二分类变量（如阴性和阳性、缓解和未缓解）或多分类变量（如治愈、显效、好转、无效）Y与一组自变量（X1,X2,…,Xp）的关系，logistic回归（logistic regression）分析是处理此类情况的有效方法。不直接分析Y与X的关系，而是分析Y取某个值的概率P与X的关系。
Logistic回归模型的参数估计采用极大似然法。
Logistic回归方程：
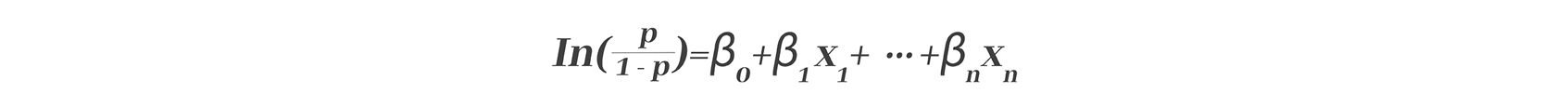
回归系数的流行病学意义是：在其他自变量都不变的条件下，当因素X变化一个测量单位时所引起的OR值自然对数的改变量。
自变量Xj增加一个单位后与增加前优势比（OR）等于eβj ,
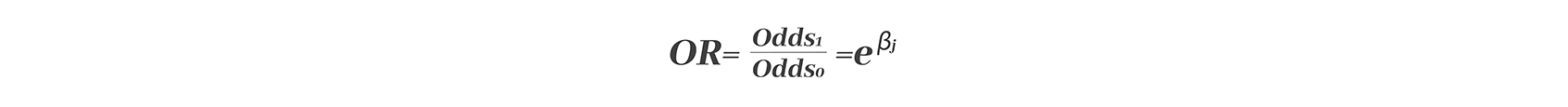
其中βj表示自变量Xj的系数。
二分类变量，一般用0和1赋值，如暴露：1，非暴露：0等，赋值较小的水平常被作为参照水平，关于这类变量的优势比就是水平1和水平0优势之比。有序多分类变量，可以按等级的秩次赋值，这样关于这类变量的优势比就是秩次k+1和秩次k的优势之比。
Logistic回归模型的参数β与流行病学研究中常用指标优势比OR有如下关系：在控制其他因素后，某一自变量X_j的二水平C1与C2（C2> C1）的优势比为OR=eβj (C2-C1)。当自变量Y=1表示患病、死亡等“坏事”发生时，若自变量Xj的回归系数βj>0，则ORj>1，则该自变量为危险因素；若βj<0，则ORj<1，该自变量为保护因素；若βj=0，则ORj=1，则该自变量对结果不起作用。
流行病学意义指的是，试验组出现结局事件的危险性是安慰剂组危险性的OR倍。由于logistic回归系数良好的可解释性，使得logistic回归在医学中特别是流行病学研究中备受欢迎。
模型应用时的注意事项
Logistic回归分析前，若样本量不多但变量多，建议先进行单变量分析（如t检验、卡方检验）考察所有自变量与因变量之间的关系，筛掉一些可能无意义的变量，再进行多因素分析，这样使得结果更为可靠。即使样本量足够大，也要弄清楚各个自变量之间的相互关系，这样才能有效的进行分析。
对临床试验数据进行Logistic回归分析时，可以借助SAS、SPSS、R软件得到专业性的结果。下面给出SAS中logistic回归分析的程序：
其中，dataset表示要分析集的SAS数据集；a1表示对应的分类变量；Y表示因变量；a1 b1表示分析中要用的自变量。
想了解更多logistic回归分析可以查看SAS软件中的“帮助”功能。
电话联系
前台客服
+8621-58301389
商务经理
+8621-56321338
邮箱
官方微信
TOP
